Tính chất hình thoi
Khái quát về hình thoi trong hệ thống tứ giác
Việc phân biệt hình thoi với các hình khác như hình chữ nhật hay hình bình hành thường dựa vào các đặc điểm về cạnh, góc và đường chéo. Khi học sinh nắm vững được khái niệm cơ bản này, việc học các phần sau như tính chất của hình thoi, công thức tính diện tích hay chứng minh tứ giác trở nên dễ dàng hơn rất nhiều.
Dấu hiệu nhận biết hình thoi trong hình học
Một tứ giác được coi là hình thoi khi nó thỏa mãn một số điều kiện quan trọng. Khi một tứ giác có bốn cạnh bằng nhau và hai đường chéo cắt nhau tại trung điểm của mỗi đường, đây là dấu hiệu rõ ràng cho thấy đó là hình thoi. Hơn nữa, hai đường chéo này còn vuông góc với nhau, tạo ra bốn tam giác vuông bằng nhau bên trong hình.
Trong thực tế, việc nhận diện hình thoi còn dựa vào quan sát sự cân đối trong hình dáng. Nếu hình tạo cảm giác nghiêng nhưng cân đối, và có thể gấp đôi qua một đường thẳng để trùng khít, rất có thể đó là hình thoi. Những hiểu biết này không chỉ giúp học sinh làm tốt các bài toán về hình học mà còn hỗ trợ trực quan khi gặp hình dạng này ngoài đời thực.
Những tính chất cơ bản mà bạn cần nắm vững
Tính chất hình thoi bao gồm nhiều đặc điểm liên quan đến cạnh, góc và đường chéo. Bốn cạnh bằng nhau là tính chất đầu tiên và quan trọng nhất. Nhờ vào điều này, hình thoi có thể dễ dàng phân biệt với hình chữ nhật hay hình bình hành thông thường. Ngoài ra, các cặp góc đối diện của hình thoi luôn bằng nhau. Điều này có nghĩa là nếu một góc nhọn thì góc đối diện cũng là góc nhọn với cùng độ lớn, tương tự với góc tù.
Hai đường chéo của hình thoi cắt nhau tại trung điểm và vuông góc với nhau. Đặc điểm này tạo ra tính đối xứng đặc biệt cho hình. Mỗi đường chéo không chỉ là đoạn nối hai đỉnh đối diện, mà còn đóng vai trò như một trục đối xứng, chia hình thành hai phần bằng nhau. Không chỉ vậy, mỗi đường chéo còn là phân giác của hai góc mà nó đi qua. Đây là điều mà không phải hình tứ giác nào cũng có được.
Vai trò của các tính chất trong bài toán hình học
Khi làm các bài toán hình học, việc hiểu và vận dụng tính chất của hình thoi là một lợi thế lớn. Học sinh có thể dùng các tính chất này để chứng minh một tứ giác là hình thoi hoặc chứng minh hai đoạn thẳng vuông góc, bằng nhau, hay chia đôi lẫn nhau. Những tính chất như đường chéo vuông góc, cắt nhau tại trung điểm và chia đôi các góc giúp việc suy luận và trình bày lời giải trở nên logic, rõ ràng và thuyết phục.
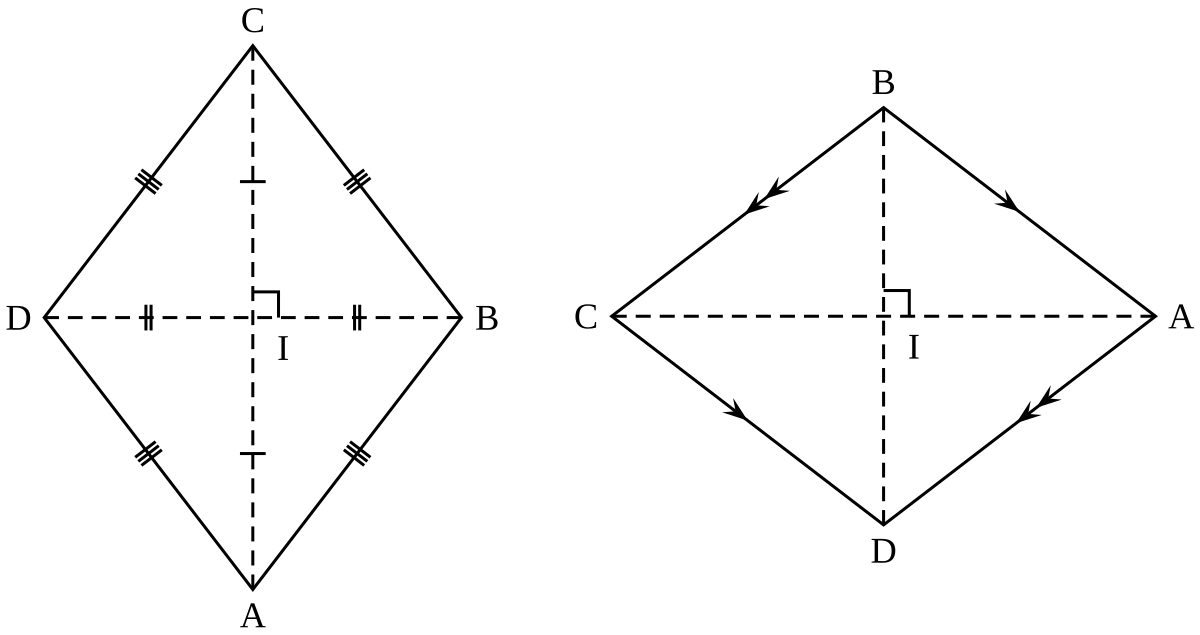
Đặc điểm quan trọng của hình thoi là hai đường chéo vuông góc và cắt nhau tại trung điểmSử dụng độ dài đường chéo để tính diện tích nhanh chóng
Tính chất của hình thoi không chỉ hữu ích trong chứng minh mà còn giúp bạn dễ dàng tính diện tích của hình này. Một trong những cách phổ biến nhất để tính diện tích hình thoi là sử dụng độ dài hai đường chéo. Khi biết độ dài đường chéo thứ nhất là d1 và đường chéo thứ hai là d2, bạn chỉ cần áp dụng công thức: S = (d1 × d2) / 2 để tính nhanh diện tích. Đây là một trong những công thức cơ bản và dễ nhớ nhất trong hình học.
Trường hợp tính diện tích bằng cạnh và góc
Ngoài công thức sử dụng đường chéo, bạn cũng có thể tính diện tích hình thoi khi biết độ dài cạnh và số đo một góc xen giữa. Khi đó, công thức áp dụng là S = a² × sin(góc), với a là độ dài cạnh hình thoi. Tuy nhiên, công thức này đòi hỏi bạn phải sử dụng hàm lượng giác sin, điều này đôi khi gây khó khăn cho học sinh chưa học đến chương trình lượng giác.
Hình minh họa công thức tính diện tích hình thoi phổ biến nhấtHình thoi trong đời sống và thiết kế
Ngoài sách vở, bạn có thể dễ dàng bắt gặp hình thoi ở nhiều nơi trong cuộc sống. Nhiều mẫu gạch lát nền, họa tiết trang trí, logo thương hiệu hay hoa văn trên quần áo đều sử dụng hình thoi vì hình dạng cân đối và dễ tạo điểm nhấn thị giác. Hình thoi còn xuất hiện trong các mô hình kỹ thuật như cơ cấu robot, thiết bị gấp gọn hay thiết kế kết cấu xây dựng nhờ tính linh hoạt và khả năng phân bố lực tốt.
Nhờ vào tính đối xứng, hình thoi không chỉ mang tính thẩm mỹ mà còn có ý nghĩa biểu tượng trong nhiều nền văn hóa. Trong các thiết kế hiện đại, người ta thường chọn hình thoi để tạo cảm giác chuyển động, tinh tế và lôi cuốn về mặt thị giác.
Tác động của hình thoi đến việc học Toán
Trong học tập, đặc biệt là môn Toán, hình thoi xuất hiện trong nhiều bài toán từ cơ bản đến nâng cao. Việc nắm vững tính chất hình thoi không chỉ giúp bạn giải bài tập nhanh hơn mà còn phát triển tư duy logic, khả năng hình dung không gian và kỹ năng chứng minh. Học sinh làm tốt phần hình thoi thường có nền tảng tốt để học các dạng bài phức tạp hơn như đường tròn nội tiếp, ngoại tiếp hay các bài toán tích hợp nhiều yếu tố hình học khác.
Khi hiểu sâu và vận dụng linh hoạt các tính chất hình thoi, bạn sẽ cảm thấy tự tin hơn khi gặp các đề bài mang tính tư duy cao. Điều này đặc biệt hữu ích với các bạn tham gia kỳ thi học sinh giỏi hoặc kỳ thi chuyển cấp.

Hình thoi được ứng dụng rộng rãi trong thiết kế đời sống thường ngày
Tính chất hình thoi là phần kiến thức cơ bản nhưng vô cùng quan trọng trong hình học. Từ khái niệm ban đầu đến các đặc điểm về cạnh, góc, đường chéo và cách tính diện tích, tất cả đều mang lại nền tảng vững chắc để bạn học tốt hơn môn Toán. Không chỉ giới hạn trong lý thuyết, hình thoi còn hiện diện trong đời sống với nhiều ứng dụng thực tiễn và thẩm mỹ.