Công Thức Cấp Số Cộng Cấp Số Nhân
Dãy số tăng hoặc giảm đều theo quy luật đơn giản
Cấp số cộng là một dãy số mà hiệu số giữa hai số hạng liên tiếp luôn bằng nhau. Nói cách khác, nếu bạn lấy bất kỳ số hạng nào trừ đi số hạng ngay trước đó thì kết quả luôn là một số không đổi. Đây được gọi là công sai (ký hiệu là d).
Ví dụ, dãy 2, 5, 8, 11, 14 là một cấp số cộng vì mỗi số sau đều lớn hơn số trước đó 3 đơn vị (d=3). Trong trường hợp công sai là số âm, dãy số sẽ giảm dần đều, chẳng hạn 20, 17, 14, 11 cũng là một cấp số cộng với công sai là -3.
Cấp số cộng thường được dùng trong bài toán tính tổng dãy số đều đặn, xác định vị trí của một số hạng cụ thể trong chuỗi, hoặc để mô tả các tình huống tăng trưởng tuyến tính trong thực tế như tiền lương tăng hàng năm theo mức cố định.

Dãy số minh họa cấp số cộng với công sai dươngTính số hạng thứ n trong cấp số cộng
Để tính một số hạng bất kỳ trong cấp số cộng, bạn có thể dùng công thức:
Un=U1+(n - 1) × d
Trong đó, U_n là số hạng thứ n, U_1 là số hạng đầu tiên, d là công sai và n là vị trí của số hạng cần tìm. Công thức này giúp bạn tìm nhanh một số hạng nằm ở bất kỳ vị trí nào trong dãy mà không cần liệt kê hết tất cả các số hạng trước đó.
Chẳng hạn, nếu dãy số bắt đầu bằng 4 và công sai là 5, để tính số hạng thứ 10, bạn chỉ cần thay vào công thức: U6=5+(6 - 1) × 4=25.
Tính tổng n số hạng đầu tiên của cấp số cộng
Tổng các số hạng đầu tiên trong cấp số cộng được tính bằng công thức:
Sn=(n × (U1 + Un)) / 2
Trong đó, S_n là tổng của n số hạng đầu tiên, U_1 là số hạng đầu tiên và U_n là số hạng thứ n.
Nếu bạn biết U_1 và công sai d nhưng chưa biết U_n, có thể dùng công thức biến đổi khác:
Sn=(n × (2U1 + (n - 1) × d)) / 2
Ví dụ, nếu dãy số bắt đầu bằng 3, công sai là 2 và bạn cần tính tổng 5 số đầu tiên, ta áp dụng: S5=(5 × (2× 3 + (5 - 1) × 2)) / 2=35
5.

Cách tính số hạng và tổng cấp số cộngDãy số nhân lên theo tỉ lệ nhất định
Cấp số nhân là một dãy số mà mỗi số hạng (trừ số đầu tiên) đều được tạo ra bằng cách nhân số trước đó với một số không đổi. Số này được gọi là công bội (ký hiệu là q).
Ví dụ, dãy 2, 4, 8, 16, 32 là một cấp số nhân vì mỗi số đều gấp đôi số trước đó (q=2). Trong trường hợp công bội là số nhỏ hơn 1 (ví dụ q=0.5), dãy số sẽ giảm dần, chẳng hạn 100, 50, 25, 12.5 cũng là cấp số nhân.
Cấp số nhân thường được dùng để mô tả sự tăng trưởng theo cấp số như lãi kép trong ngân hàng, sự phát triển của vi khuẩn, hoặc tốc độ tăng dân số trong điều kiện lý tưởng.
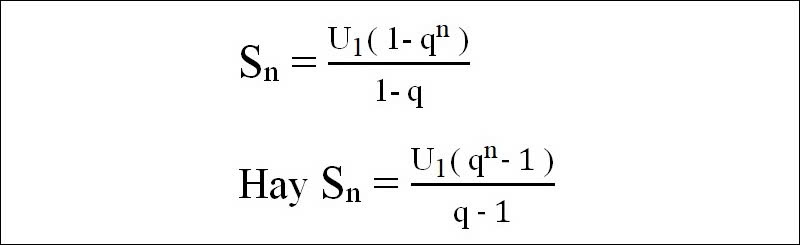
Biểu đồ minh họa cấp số nhân tăng theo lũy thừaTính số hạng thứ n trong cấp số nhân
Để tìm một số hạng bất kỳ trong cấp số nhân, bạn dùng công thức:
Un=U1 × q^(n - 1)
Trong đó, U_n là số hạng thứ n, U_1 là số đầu tiên và q là công bội. Công thức này đặc biệt hữu ích khi bạn cần tìm số lớn trong chuỗi mà không phải nhân nhiều lần thủ công.
Ví dụ, nếu số đầu là 3 và công bội là 2, số hạng thứ 5 là: U5=3 × 2^(5 - 1)=3 × 16=48.
Tính tổng n số hạng đầu tiên của cấp số nhân
Tổng n số hạng đầu trong cấp số nhân được tính theo công thức:
Sn=U1 × (q^n - 1) / (q - 1) nếu q khác 1
Trong trường hợp công bội là 1, dãy số lặp lại và tổng n số hạng chỉ đơn giản là n x 1.
Ví dụ, dãy bắt đầu bằng 2, công bội là 3, tổng 4 số đầu là: S4=2 × (3^4 - 1) / (3 - 1)=80.
Cách tăng trưởng tuyến tính và tăng trưởng theo cấp số
Cấp số cộng mô tả các tình huống tăng trưởng đều đặn theo thời gian, chẳng hạn mức tiết kiệm bạn bỏ vào mỗi tháng là 1 triệu đồng, sau 12 tháng bạn có tổng cộng 12 triệu đồng nếu không tính lãi. Đây là một ví dụ kinh điển của cấp số cộng với công sai bằng một triệu.
Ngược lại, cấp số nhân phản ánh sự tăng trưởng theo cấp số – càng về sau càng tăng nhanh. Ví dụ, nếu bạn đầu tư 1 triệu đồng mỗi tháng và số tiền đó được nhân đôi sau mỗi năm do lãi kép, số tiền sau 5 năm sẽ không đơn thuần là gấp 5, mà là 1 triệu nhân với 2 lũy thừa 5, tạo nên sự gia tăng vượt trội. Đây chính là sự khác biệt cơ bản giữa hai loại cấp số.
Việc phân biệt đúng công thức cấp số cộng cấp số nhân này không chỉ giúp bạn làm bài toán đúng mà còn giúp bạn hiểu và áp dụng kiến thức vào đời sống thực tế, từ tài chính cá nhân đến quản lý dự án, từ tăng trưởng học tập đến phân tích dữ liệu.
Cấp số cộng và cấp số nhân là hai kiến thức cơ bản nhưng rất quan trọng trong chương trình toán học phổ thông. Việc nắm vững công thức cấp số cộng cấp số nhân sẽ giúp bạn dễ dàng giải quyết các bài toán từ cơ bản đến nâng cao và ứng dụng vào thực tế như tiết kiệm, đầu tư, sản xuất, tăng trưởng học tập. Hãy luyện tập đều đặn và đừng ngần ngại hỏi khi gặp khó khăn – vì hiểu đúng bản chất, bạn sẽ học toán dễ dàng hơn rất nhiều.